O que é Tautologia? Veja os exemplos!
A tautologia é um dos assuntos mais cobrados nas provas de concurso em raciocínio lógico. Por isso, neste artigo veremos o que é Tautologia, alguns exemplos e exercícios para treinar!
Porém, antes de iniciarmos esse assunto é importante entender alguns conceitos preliminares sobre a tautologia. Então, vamos lá!
O que é uma tautologia no raciocínio lógico?
Quando falamos em lógica, a tautologia é uma proposição composta que tem sempre valor lógico verdadeiro.
Para entender melhor os casos de tautologia, é recomendado construir tabelas verdade durante a resolução de problemas para evitar erros.
Dessa maneira, podemos concluir que existem inúmeras expressões que são tautologias. Vejamos alguns exemplos.
O que é tautologia exemplo?
Para compreender melhor o conceito de tautologia é importante conferirmos alguns exemplos:
Exemplo 1:
O exemplo mais simples é a proposição p v (~p), sendo assim, qualquer que seja o valor lógico da proposição p, essa proposição sempre será verdadeira. Veja a afirmação:
“João é sério ou João não é sério”
Note que essa proposição sempre será verdadeira.
Exemplo 2:
Neste exemplo temos (p ∧ q) → (p ↔ q) sendo:
“Se João é sério e Maria é falante, então João é sério se e somente se Maria for falante.”
Conforme podemos ver essa proposição se trata claramente de uma Tautologia.
Em resumo, na dedução lógica, uma tautologia é uma verdade óbvia e que nada acrescenta em termos de conhecimento de mundo para auxiliar a demonstração de alguma sentença.

Como reconhecer uma tautologia?
Para reconhecer uma tautologia é necessário preencher a tabela verdade, isso facilita bastante.
Pois com a tabela basta analisar a última coluna, dessa forma, caso a coluna da proposição analisada tenha somente valores lógicos verdadeiros, ela será uma tautologia.
Proposição o que é?
Embora já tenha mencionado anteriormente, é importante enfatizar que a base do estudo de Raciocínio Lógico é a proposição.
Sendo assim, uma proposição sempre será falsa ou verdadeira. Por exemplo: “A bola é vermelha.”
Perceba que esta é uma proposição que poderá ter valor lógico falso ou verdadeiro, dependendo do contexto.
Proposições compostas
As proposições compostas, como o nome já diz, nada mais é que a utilização de mais de uma proposição na mesma frase. Exemplo:
“O carro é vermelho e a roda é preta.”
Simbolicamente, podemos representar essa proposição da seguinte maneira: p ∧ q.
Agora, vejamos outros conceitos importantes:
Contradição e Contingência
Se você já prestou concurso público já deve ter se deparado com questões em que além da tautologia foi cobrado também outros dois assuntos: Contradição e Contingência.
Falaremos brevemente sobre esses assuntos apenas para que você possa discernir melhor quando encontrar tais questões.
Contradição: o que é?
Quando falamos em Contradição entendemos que se trata de uma proposição lógica composta que é sempre falsa. Veja o exemplo:
“Marcos é homem e Marcos não é homem.”
No caso deste exemplo temos que a contradição consiste em afirmar algo e depois negar essa mesma afirmação durante sua argumentação.
Podemos representar essa proposição da seguinte forma: p ∧ (~p).
Contingência: o que é?
Quando pensamos no caso mais comum de proposição lógica, logo vem à cabeça a Contingência.
Pois ela consiste numa proposição composta que pode ser verdadeira ou falsa, dependendo do valor lógico das premissas que a constituem.
Nesse caso, se enquadram a maioria das proposições. Veja o exemplo:
“Sérgio é brasileiro e é mestre em filosofia.”
O exemplo acima pode ser representado por p ∧ p.
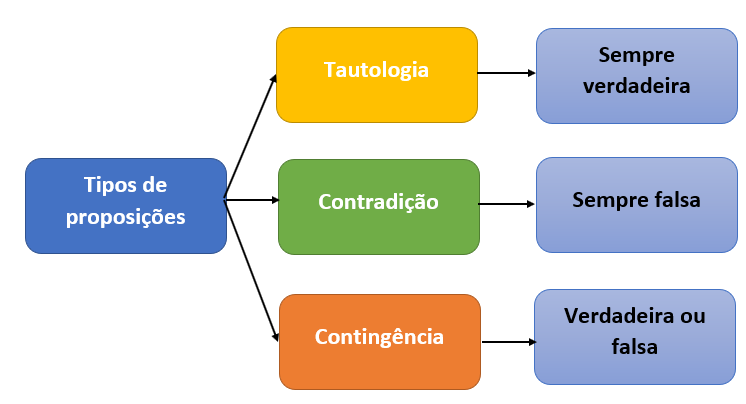
Veja o esquema abaixo para nunca mais errar:
Agora, confira algumas questões cobradas em provas de concurso e depois corrija com o gabarito. Vamos treinar!
Questões de concurso sobre Tautologia
Questão 1 – Fepese (2022)
Assinale a alternativa que representa corretamente uma tautologia.
(A) João é rico ou Emília é pobre.
(B) João é magro e João não é magro.
(C) João é magro ou João não é magro.
(D) Ou José é rico ou Maria é estudiosa.
(E) Se x é um número real maior que 2, então x é menor que 2.
Questão 2 – Instituto AOCP (2022)
Assinale a alternativa cuja proposição NÃO é uma tautologia.
(A) p∨∼p
(B) (p∧q)→(p↔q)
(C) p→(p∨q)
(D) (p∧q)→(p∨q)
(E) (p→q)∧(p∨q)
Questão 3 – Quadrix (2022)
Sendo p, q e r três proposições, julgue o item.
A proposição (p∨∼q)↔(∼p∧q) é uma tautologia.
(C) Certo
(E) Errado
Questão 4 – Quadrix (2022)
Julgue o item.
A proposição “Bárbara é brasileira ou Bárbara não é brasileira” é uma tautologia.
(C) Certo
(E) Errado
Questão 5 – Instituto AOCP (2022)
Considerando as proposições compostas e, por consequência, os conectivos lógicos, é possível determinar diversas estruturas para as quais se podem avaliar os valores-verdade. Assim, é correto afirmar que duas proposições compostas são equivalentes somente se suas tabelas-verdade têm, como resposta, a mesma sequência de valores lógicos.
Nesse contexto, sendo P1 e P2 proposições compostas equivalentes, assinale a alternativa na qual sempre figuram tautologias.
(A) P1 ˄ P2 e P1 ˅ P2
(B) P1 ˅ P2 e P1 → P2
(C) P1 → P2 e P1 ↔ P2
(D) P1 ↔ P2 e P1 ˄ P2
(E) ~P1 e ~P2
Gabarito:
- Questão 1 – Resposta correta: letra C
- Questão 2 – Resposta correta: letra E
- Questão 3 – Resposta correta: Errado
- Questão 4 – Resposta correta: Certo
- Questão 5 – Resposta correta: letra C
